Разлика между B-дърво и двоично дърво

2019

B-tree и Binary tree са видовете нелинейна структура на данните. Въпреки че термините изглеждат сходни, но са различни във всички аспекти. Двоично дърво се използва, когато записите или данните се съхраняват в RAM вместо на диска, тъй като скоростта на достъп до RAM е много по-висока от тази на диска. От друга страна, B-дървото се използва, когато данните се съхраняват в диска и намалява времето за достъп, като намалява височината на дървото и увеличава клоновете в възела.

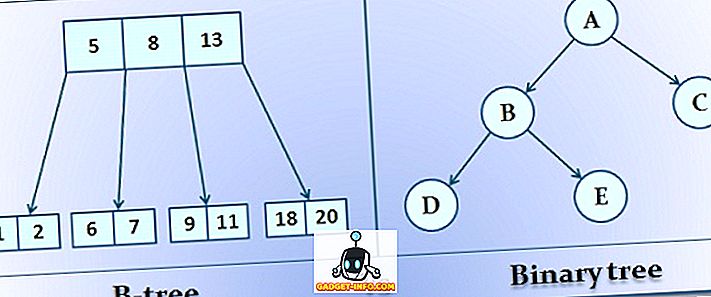
Друга разлика между B-дървото и двоичното дърво е, че B-дървото трябва да има всички негови детски възли на едно и също ниво, докато двоичното дърво няма такова ограничение. Двоичното дърво може да има максимум 2 поддерева или възли, докато в B-дървото може да има M no от поддерев или възли, където M е редът на B-дървото.

Сравнителна таблица

Основа за сравнение	B-дърво	Двоично дърво
Съществено ограничение	Възел може да има най-много M брой дъщерни възли (където M е реда на дървото).	Един възел може да има максимум 2 броя под-дървета.
Използва се	Използва се, когато данните се съхраняват на диск.	Използва се, когато записите и данните се съхраняват в RAM.
Височина на дървото	log `_M` N (където m е реда на дървото M-way)	log `₂` N
Приложение	Структурата на данните за индексиране на кодове в много СУБД.	Оптимизиране на код, кодиране на Huffman и др.

Дефиниция на В-дърво

B-дървото е балансираното дърво на M-way и е известно също като балансирано сортирано дърво. Той е подобен на двоичното дърво за търсене, където възлите са организирани на базата на прехвърлянето. Пространствената сложност на B-дървото е O (n). Времевата сложност на вмъкване и изтриване е O (log n).

Има определени условия, които трябва да са верни за B-дърво:

Височината на дървото трябва да е възможно най-малка.
Над листата на дървото не трябва да има никакви празни под-дървета.
Листата на дървото трябва да са на едно и също ниво.
Всички възли трябва да имат най-малък брой деца, освен да напускат възли.

Свойства на B-дърво от ред M

Всеки възел може да има максимум М брой деца и минимален брой М / 2 деца или всяко число от 2 до максимум.
Всеки възел има по един ключ по-малък от децата с максимални M-1 ключове.
Подреждането на ключовете е в някакъв специфичен ред в рамките на възлите. Всички ключове в поддървото, което се намира в лявата част на ключа, са предшественици на ключа, и това, което присъства в дясната част на ключа, се наричат наследници.
По време на вмъкването на пълен възел, дървото се разделя на две части, а ключът със средна стойност се вмъква в родителския възел.
Операцията по сливане се извършва, когато възлите са изтрити.

Дефиниция на двоичното дърво

Двоичното дърво е дървовидна структура, която може да има най-много две указатели за своите детски възли. Това означава, че най-високата степен, която един възел може да има, е 2 и може да има и нула или един градус възел.

Има някои варианти на двоично дърво, като строго двоично дърво, пълно двоично дърво, разширено двоично дърво и т.н.

Строго двоичното дърво е дърво, където всеки не-терминален възел трябва да има ляво поддърво и дясно поддърво.
Дърво се нарича Пълно двоично дърво, когато отговаря на условието да има 2 i възли на всяко ниво, където i е нивото.
Нишковиден двоичен е двоично дърво, което се състои от 0 или 0 от възли.

Техники на траверса

Преминаването на дървото е една от най-честите операции, извършвани в дървовидна структура на данни, в която всеки възел е посещаван точно веднъж по систематичен начин.

Inorder- В това пресичане на дървото левият поддърво се посещава рекурсивно, след което се разглежда коренния възел и в последното дясно поддърво се посещава.
Preorer- В това пресичане на дървото коренният възел се посещава първо след това вляво поддърво и най-накрая дясно поддърво.
Постери - Тази техника посещава ляво поддърво, след това дясно поддърво и най-накрая корен.

Ключови разлики между B-дърво и двоично дърво

В B-tree максималният брой на детските възли, които може да има не-терминален възел, е M, където M е редът на B-дървото. От друга страна, двоичното дърво може да има най-много две поддерева или детски възли.
B-tree се използва, когато данните се съхраняват на диск, докато двоичното дърво се използва, когато данните се съхраняват в бърза памет като RAM.
Друга област на приложение за B-tree е структурата на данните за индексиране на кодове в СУБД, за разлика от това бинарното дърво се използва в оптимизацията на кода, кодирането на huffman и др.
Максималната височина на B-дървото е log _M N (M е реда на дървото). Максималната височина на двоичното дърво е log ₂ N (N е броят на възлите, а базата е 2, защото е за двоичен).

заключение

B-дървото се използва над двоично и двоично дърво за търсене, като основната причина за това е йерархията на паметта, където CPU е свързан с кеш с канали с висока честотна лента, докато CPU е свързан към диск чрез канал с ниска честотна лента. Двоично дърво се използва, когато записите се съхраняват в RAM (малки и бързи) и B-дървото се използва, когато записите се съхраняват на диск (голям и бавен). Така че използването на B-tree вместо Binary tree значително намалява времето за достъп поради висок коефициент на разклоняване и намалена височина на дървото.