Разлика между вариацията и стандартното отклонение

2019

Дисперсията показва степента, в която наблюденията се отклоняват от подходяща мярка за централна тенденция. Мерките на дисперсията попадат в две категории, т.е. абсолютна мярка на дисперсията и относителна мярка на дисперсията. Дисперсията и стандартното отклонение са два вида абсолютна мярка за променливост; който описва как наблюденията са разпределени около средната стойност. Отклонението не е нищо друго освен средната стойност на квадратите на отклоненията,

За разлика от стандартното отклонение е квадратен корен от цифровата стойност, получена при изчисляване на дисперсията. Много хора противопоставят тези две математически понятия. Така, тази статия прави опит да се хвърли светлина върху важната разлика между вариацията и стандартното отклонение.

Сравнителна таблица

Основа за сравнение	вариране	Стандартно отклонение
значение	Отклонението е числова стойност, която описва променливостта на наблюденията от средноаритметичната му стойност.	Стандартното отклонение е мярка за дисперсията на наблюденията в рамките на набор от данни.
Какво е?	Това е средната стойност на квадратите отклонения.	Това е средното квадратично отклонение.
Етикетирани като	Сигма-квадрат (σ ^ 2)	Сигма (σ)
Изразено в	Квадрати единици	Същите единици като стойностите в набора от данни.
Показва	Колко далече са хората в групата.	Колко наблюдения на набор от данни се различават от средните.

Дефиниция на отклонение

В статистиката, дисперсията се определя като мярка за променливост, която представлява колко далеч са разпределени членовете на групата. Той установява средната степен, до която всяко наблюдение варира от средното. Когато дисперсията на масива от данни е малка, тя показва близостта на данните към средната стойност, докато по-голямата стойност на дисперсията показва, че наблюденията са много разпръснати около средноаритметичното и един от друг.
За некласифицирани данни :

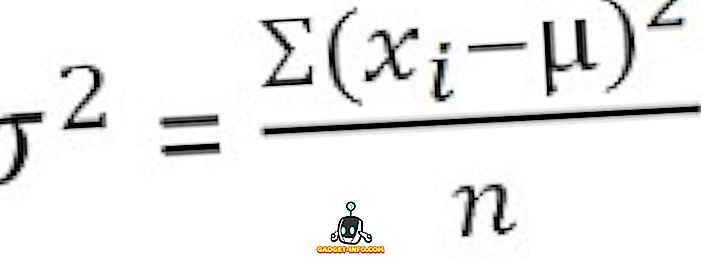
За групирано разпределение на честотата :

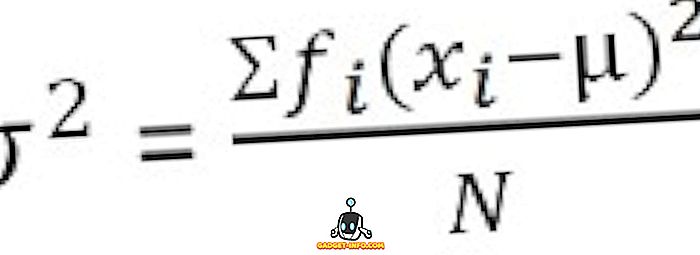
Дефиниция на стандартното отклонение

Стандартното отклонение е мярка, която определя количеството дисперсия на наблюденията в набор от данни. Ниското стандартно отклонение е индикатор за близостта на резултатите до средноаритметичното и представлява високо стандартно отклонение; резултатите са разпръснати в по-висок диапазон от стойности.
За некласифицирани данни :

За групирано разпределение на честотата :

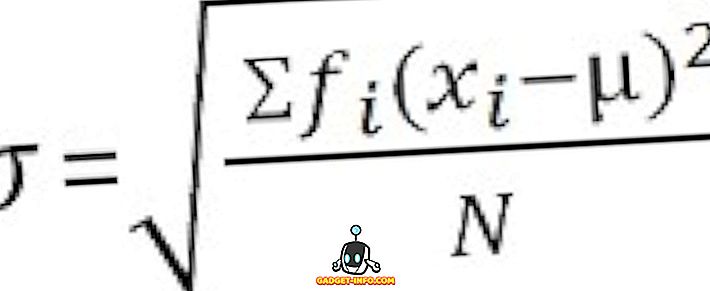
Ключови разлики между вариация и стандартно отклонение

Разликата между стандартното отклонение и вариацията може да се направи ясно на следните основания:

Отклонението е числова стойност, която описва променливостта на наблюденията от средноаритметичната му стойност. Стандартното отклонение е мярка за дисперсията на наблюденията в рамките на набор от данни.
Отклонението не е нищо друго освен средната стойност на квадратите отклонения. От друга страна, стандартното отклонение е средното квадратично отклонение.
Дисперсията се обозначава със сигма-квадрат (σ2), докато стандартното отклонение е означено като сигма (σ).
Отклонението се изразява в квадратни единици, които обикновено са по-големи от стойностите в дадения набор от данни. За разлика от стандартното отклонение, което се изразява в същите единици като стойностите в набора от данни.
Вариантът измерва колко далеч са разпределени индивидите в групата. Обратно, стандартното отклонение измерва колко наблюдения на даден набор от данни се различават от средните.

Илюстрация

Оценките, отбелязани от един ученик в пет предмета, са съответно 60, 75, 46, 58 и 80. Трябва да откриете стандартното отклонение и дисперсия.
Първо, трябва да разберете средното,

Така средните (средни) оценки са 63.8
Сега изчислете вариацията

х	А	(Ха)	(ХА) ^ 2
60	63.8	-3, 8	14.44
75	63.8	11.2	125, 44
46	63.8	-17.8	316, 84
58	63.8	5.8	33.64
80	63.8	16.2	262, 44

Където X = наблюдения
А = аритметична средна стойност

Така че вариацията е 150.56

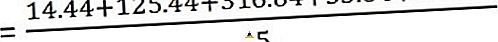
А стандартното отклонение е -

прилики

И двете вариации и стандартно отклонение са винаги положителни.
Ако всички наблюдения в набор от данни са идентични, тогава стандартното отклонение и дисперсия ще бъдат нула.

заключение

Тези два са основни статистически термини, които играят жизненоважна роля в различни сектори. Стандартното отклонение е за предпочитане пред средното, тъй като е изразено в същите единици като тези на измерванията, докато дисперсията е изразена в единиците, по-големи от дадения набор от данни.