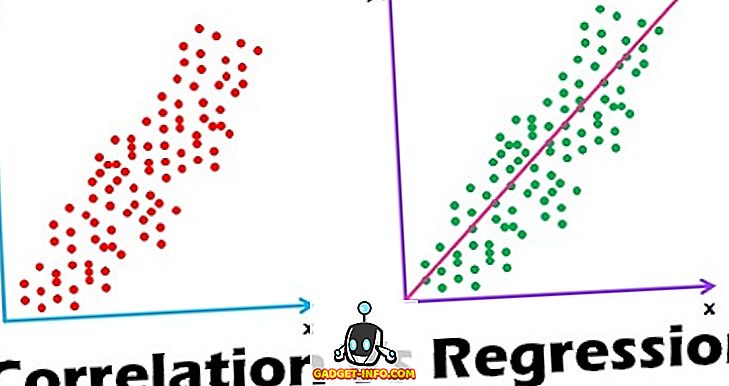
Разликата между корелация и регресия е един от често задаваните въпроси в интервютата. Нещо повече, много хора изпитват неяснота в разбирането на тези две неща. Така че, вземете пълно четене на тази статия, за да имате ясно разбиране за тези две.
Сравнителна таблица
| Основа за сравнение | корелация | регресия |
|---|---|---|
| значение | Корелацията е статистическа мярка, която определя съотношението или асоциацията на две променливи. | Регресия описва как една независима променлива е числено свързана с зависимата променлива. |
| употреба | Да представлява линейна връзка между две променливи. | За да се побере най-добрата линия и да се оцени една променлива въз основа на друга променлива. |
| Зависими и независими променливи | Няма разлика | И двете променливи са различни. |
| Показва | Коефициентът на корелация показва степента, до която две променливи се движат заедно. | Регресията показва въздействието на промяната на единица в известната променлива (x) върху оценената променлива (y). |
| Обективен | Да се намери цифрова стойност, изразяваща връзката между променливите. | Да се оценят стойностите на случайната променлива въз основа на стойностите на фиксираната променлива. |
Дефиниция на корелация
Терминът корелация е комбинация от две думи „Co“ (заедно) и връзка (връзка) между две величини. Корелацията е когато, по време на проучването на две променливи, се наблюдава, че промяната на единица в една променлива се отвръща чрез еквивалентна промяна в друга променлива, т.е. пряка или непряка. В противен случай се казва, че променливите са некоррелирани, когато движението в една променлива не се равнява на движение в друга променлива в определена посока. Това е статистическа техника, която представя силата на връзката между двойките променливи.
Корелацията може да бъде положителна или отрицателна. Когато двете променливи се движат в една и съща посока, т.е. увеличението на една променлива ще доведе до съответното увеличение на друга променлива и обратно, тогава променливите се считат за положително корелирани. Например : печалба и инвестиции.
Напротив, когато двете променливи се движат в различни посоки, по такъв начин, че увеличението на една променлива ще доведе до намаляване на друга променлива и обратно, тази ситуация е известна като отрицателна корелация. Например : Цена и търсене на продукт.
Мерките за корелация са дадени като:
- Коефициентът на корелация на продукта на Карл Пирсън
- Коефициент на рангова корелация на Spearman
- Диаграма на разсейване
- Коефициент на едновременни отклонения
Определение на регресия
Статистическа техника за оценка на промяната в метричната зависима променлива, дължаща се на промяната в една или повече независими променливи, базирана на средната математическа връзка между две или повече променливи, е известна като регресия. Той играе важна роля в много човешки дейности, тъй като е мощен и гъвкав инструмент, който използва за прогнозиране на минали, настоящи или бъдещи събития въз основа на минали или настоящи събития. Например : Въз основа на минали записи може да се изчисли бъдещата печалба на бизнеса.
При проста линейна регресия има две променливи x и y, където y зависи от x или say, повлияни от x. Тук y се нарича зависима, или променлива критерий, а x е независима или променлива променлива. Регресионната линия на y на x се изразява в:
y = a + bx
където, а = константа,
b = коефициент на регресия,
В това уравнение a и b са два параметъра на регресия.
Основни разлики между корелацията и регресията
Посочените по-долу точки обясняват разликата между корелация и регресия в детайли:
- Статистическа мярка, която определя съотношението или асоциацията на две величини, е известна като корелация. Регресия описва как една независима променлива е числено свързана с зависимата променлива.
- Използва се корелация, за да се представи линейната зависимост между две променливи. Напротив, регресията се използва, за да се побере най-добрата линия и да се оцени една променлива въз основа на друга променлива.
- В корелация няма разлика между зависимите и независимите променливи, т.е. корелацията между x и y е подобна на y и x. Обратно, регресията на y върху x е различна от x на y.
- Корелацията показва силата на връзката между променливите. За разлика от това, регресията отразява влиянието на промяната на единицата в независимата променлива върху зависимата променлива.
- Корелацията цели да намери цифрова стойност, която изразява връзката между променливите. За разлика от регресия, чиято цел е да се предскажат стойности на случайната променлива на базата на стойностите на фиксираната променлива.
заключение
С горната дискусия е очевидно, че има голяма разлика между тези две математически понятия, въпреки че тези две са изучени заедно. Корелацията се използва, когато изследователят иска да знае, че дали изследваните променливи са корелирани или не, ако да, тогава каква е силата на тяхната асоциация. Коефициентът на корелация на Пиърсън се счита за най-добрата мярка за корелация. При регресионен анализ се установява функционална връзка между две променливи, така че да се правят бъдещи прогнози за събитията.